

Chandrayaan-3, the remarkable lunar mission, is our country’s epitome of brilliance and persistence. The voyage takes us through fundamental scientific principles, cutting-edge technology, and the incredible soft-landing process on the Moon’s South Pole. The space mission aligns with the country’s ethos ‘The world is one’. India’s scientific achievements in space are not to lead the space race. Instead, our achievements are for the benefit of all humankind.
Chandrayaan-3 is the third lunar exploration mission of India. Students who aspire to pursue STEM (Science, Technology, Engineering, and Mathematics) can explore fundamental physics concepts of gravity, motion, propulsion, etc. The process also urges students to think critically and develop problem-solving skills. This mission also highlights the cross-disciplinary nature of space science and motivates students to identify the way multiple fields of knowledge intersect and collaborative approaches that aid real-world scientific pursuits.
As suggestive of its name, Astrodynamics is a field of study within Aerospace Engineering and Physics that encompasses the study of motion and dynamics of objects in space. It focuses on an array of principles and calculations about spacecraft behaviours, satellites, planets, and celestial body movement in the cosmos. Astrodynamics has a vital role in mission planning, satellite orbit determination, and spacecraft navigation. The orbital mechanics, gravitational interactions, propulsion systems, and trajectory planning determine the successful execution of space missions. Astrodynamics also drives technological advancements that further our progress in space exploration.
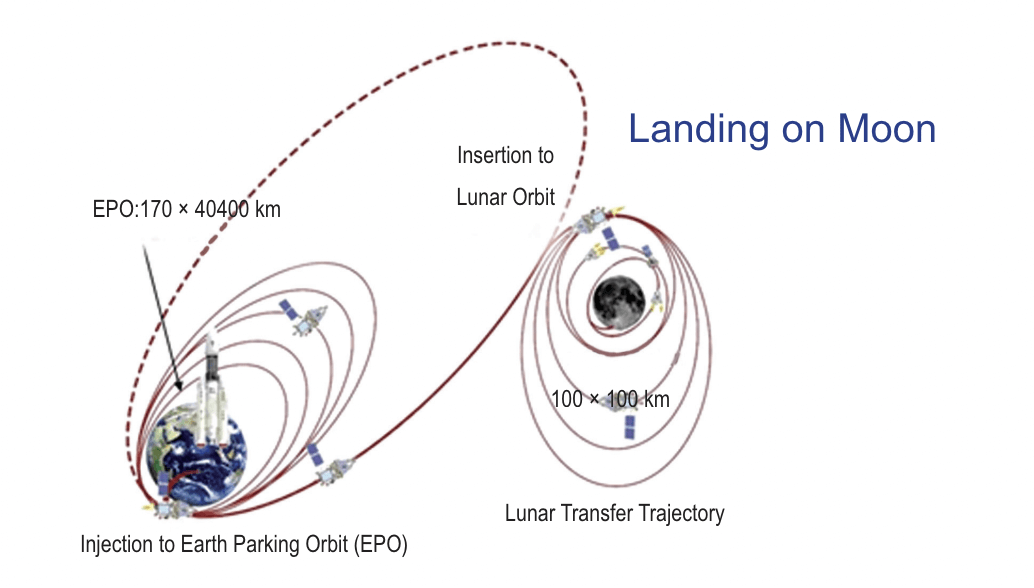
The Chandrayaan-3 was launched using a spacecraft known as ‘Bahubali’ and a Launching Vehicle (LVM3-M4). It was launched from the Satish Dhawan Space Center (SHAR), Sriharikota, Andhra Pradesh.
Let's break this down for simple understanding. Any rocket has to possess a massive amount of energy to overcome the gravitational pull of the Earth. Then, it has to periodically increase its speed until the desired speed is reached. This allows it to be slingshot into the gravitational field of the Moon.
Upon reaching the orbit of the Moon, the rocket has to lose speed till the orbit becomes circular, and a soft landing on the Moon is possible.
For a better understanding, let's take the analogy of a velodrome.

The stunt man in this velodrome, alternatively known as the wall of death, is able to maintain his vehicle’s grip on the wall due to friction and centripetal force. The shape of the velodrome is similar to that of a frustum, a sliced cone. The vertex of the cone is like a bucket.
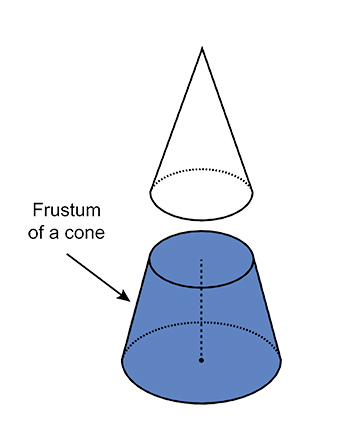
The orbit of the rider is a plane intersecting the axis of the velodrome. The rider moves in an elliptical path. If the rider increases the speed of his movement periodically, he gains kinetic energy that overcomes the gravitational pull of the earth and rises almost up to the brim of the velodrome gradually.
The above analogy can now be applied to the rocket. If the rocket has to carry out a trans-lunar journey, the Chanrayaan is also supposed to increase its speed to reach the gravitational field of the moon.
Now let's imagine that there is another velodrome nearby and our biker has to enter this velodrome and land safely on the floor. Till the brim of the initial velodrome, the biker had to maintain a high speed. Now to enter another velodrome, they would need to decrease their speed in order to land on the floor safely.
Adding another level of difficulty to this scenario, let's assume that the second velodrome is moving around the initial velodrome. If the biker gets out of the stationary initial velodrome early or too late relative to the circling one, he would ill-fatedly crash land. Physics plays a major and crucial role in calculating the exact point, timing, and speed of ejection and ensuring safe landing.
According to the ‘Reduced Mass’ concept in physics, the equations of motion of two interacting bodies can be reduced to a single equation that describes the motion of one body. The reference frame is centred on the other body. The moving body will behave as if its mass were the product of two masses divided by their sum. This quantity is called the effective reduced mass.
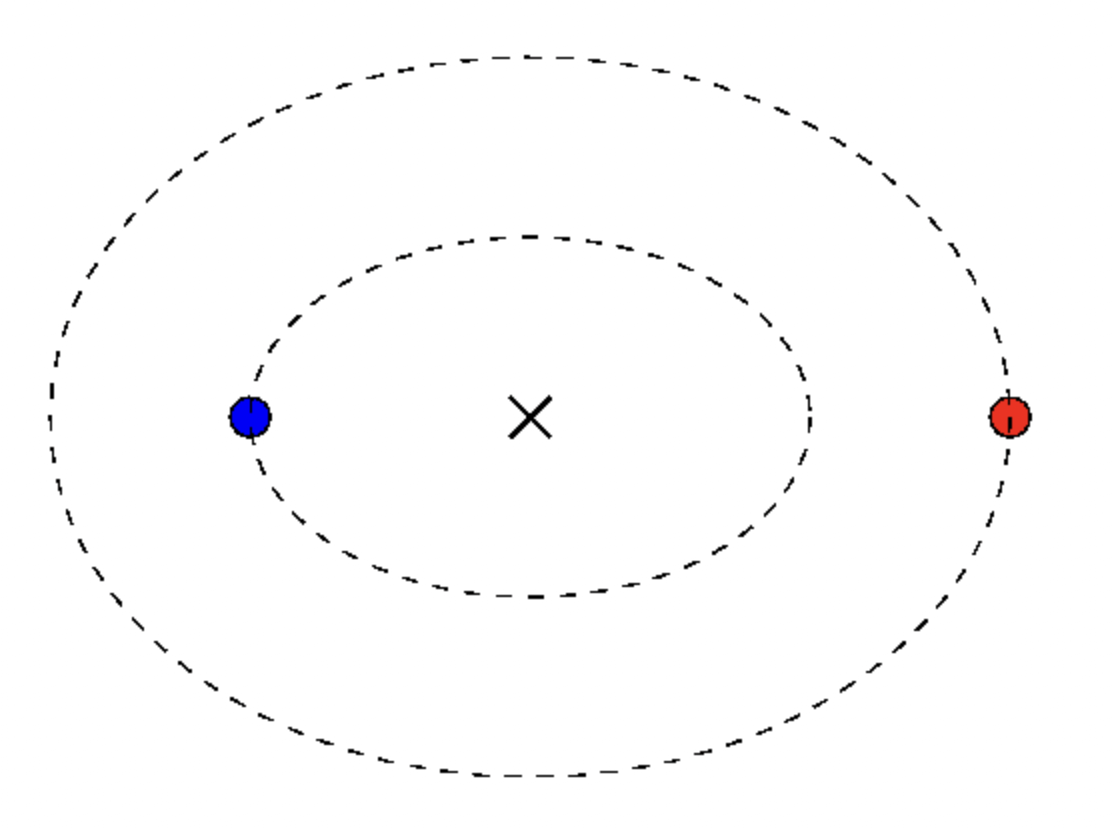
Hence, the two-body problem (Earth and Moon) is a one-body problem.
In Chandrayaan’s case, its mass is negligible compared to the mass of the Earth or the Moon. So we do not need to consider reduced mass. The Chandrayaan has both radial and angular speed. Along a straight line, linear motion applies. Angular motion remains zero. In a circular motion, a moving particle’s distance from the centre remains constant, hence its radial speed is zero.
In rocket/satellite dynamics, the distance from the centre and the angle position keep changing. Therefore, both angular and radial speeds are non-zero. The angular momentum of the satellite is under the influence of gravitational force. Therefore, the orbit of a satellite under a central force is conical (hyperbole/ellipse/circle/parabole). But the actual path it takes depends on the eccentricity and energy/speed of the satellite. Eccentricity, in this case, is nothing but a measure of the deviation of the curve from the circularity of the given shape. When the satellite keeps circuiting in the same path, the path is called the orbit. If it just passes once through any path, it is called a trajectory.
To understand the above better, let us take the analogy of a torchlight. When the torch illuminates a wall at different angles, observe the shapes of the silhouettes. These different shapes represent the conic section of movement of the satellite in its desired orbit.
Let us delve into the physics behind a rocket’s motion. The instant mass of the rocket would also include the mass of the fuel. When the rocket is stationary, the rocket’s velocity and the exhaust gas velocity are zero. But on movement, a particular mass of the exhaust gas is expelled out and there is a decrease in the weight of the rocket.
In space, the external force on the rocket and exhaust gas is negligible. Therefore the rocket and exhaust gases can be considered as a closed entity and linear momentum can be conserved.
When fuel usage of the rocket is increased by 5%, say from 75% to 80%, the final rocket velocity increases by 1.38 times to 1.6 times. But when the usage is increased by 5% from 90% to 95%, the final rocket velocity drastically jumps from 2.3 to 6.9 times. This is due to the no nonlinear logarithmic nature of the rocket equation. The analogy that makes understanding easier here is an inflated cucumber-shaped balloon with a straw glued to it along its axis.
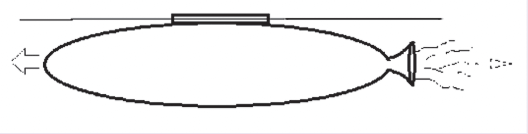
Let's affix a thread to the wall or table and have the other end of the thread go through the straw on the inflated balloon. Now the other end of the thread is affixed to another table or wall, the thread is to be left slightly taut. When the balloon is released, the pressurised air escapes from the balloon, and the balloon rocket moves along the thread. When the nozzle of the balloon is reduced, the pressurised air would have a lesser flow for a greater amount of time.
According to Newton’s second law of motion, the greater the mass of rocket fuel burnt, the faster the gas produced can escape the engineer which leads to a greater thrust of the rocket.
To achieve high speed, a rocket can be divided into multiple stages, the velocity achieved in each stage is cumulative. Depending on the speed desired, stages can be increased but after a particular stage, assembling the rocket will not be pragmatic. The Chandrayaan-3 is a three-stage rocket. The mass breakdown of each stage of the rocket is given below.
| Composition | Stage I | Stage II | Stage III |
| Fuel | 6300 kg | 630 kg | 63 kg |
| Rocket Body | 2700 kg | 270 kg | 27 kg |
| Payload | 1000 kg | 100 kg | 10 kg |
| Total | 10,000 kg | 1000 kg | 100 kg |
| Total mass at launch = 10,000 kg | |||
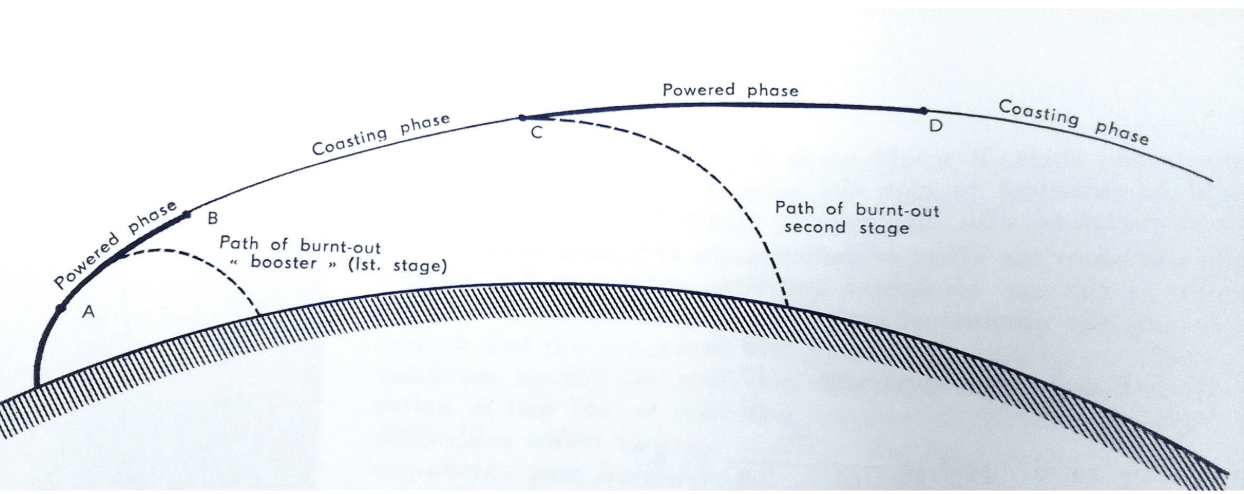
At the first stage, maximum thrust needs to be provided as the rocket has to fight against atmospheric pressure. The rocket has to travel the least amount of distance through the earth’s thick atmosphere. The rocket is fired vertically during the launch and has to attain its orbit. The rocket reaches the upper atmosphere in the least amount of time, known as the powered phase. At this point, the first stage of the rocket is dropped or jettisoned. By virtue of inertia alone, the rocket keeps moving in the coasting phase at a predetermined speed and altitude after which, second-stage ignition happens that sets the rocket in an elliptical orbit.
Chandrayaan-3 is launched vertically to minimise air drag. After a certain altitude, the trajectory comes into play. When the rocket is inclined, there is no braking system. A couple acts about the center of mass of the rocket which can somersault the rocket. The fins of the rocket are used in the upper atmosphere or space where there is little air. The rocket is given a slight turn at the axis to maintain a gyroscopic effect and be stable.
There are auxiliary rockets called vernier rockets. These are used to stabilise and incline the rocket.
The rocket also gains speed due to the rotation of the earth. This is called maximum linear speed. This is at its maximum on the equator where the axis of rotation is maximum. Hence the Chandrayaan-3 should be launched along the eastern direction close to the equator to gain additional speed of rotation of the earth.
After reaching the gravitational neutral point of the Earth-Moon system, which is an imaginary position on the imaginary line that joins the centre of the Earth and Moon, the gravitational field intensity of both the Earth and the Moon are the same.
This point is nine-tenth of the distance of separation of the Earth and the Moon. Its distance from the Earth is approximately 345000 km and 3800 km from the moon. The moon travels at a distance of 3600 km in one hour.
Hence if the Chandrayaan reaches this point by an error of 1 hour, it will miss the moon. Even with a negligible error in the launching speed, the rocket may miss the moon.
Hence propulsion module after the rocket is inserted in the lunar gravitational field, has to be slowed down. This slowing down is achieved by retro rockets. Periodic action of retro rockets ensures the decrease of the propulsion. For the final orbit before soft landing, the propulsion module needs to be anchored in a circular orbit close to the moon.
The lunar terrain is scouted for a proper harbouring point at the moon’s south pole. The lander module Vikram then detaches from the propulsion module and descends onto the moon.
The descent is controlled by onboard computers and ground stations that receive velocities and position of the Vikram with no control on landing. India finally became the fourth country to land on the moon and the first to carry out a soft landing near the south pole of the moon. The landing point is named Shiv Shakti.
While calculations are not included in this write-up, it is an attempt to simplify the understanding of the entire mission that has been our Nation’s historical feat.

JAIN PU College, a part of the renowned JGI Group, is committed to empowering students with quality education.
Beyond academics, the college ensures its online content reflects the same standard of excellence. Every blog and article is meticulously vetted and proofread by subject matter experts to ensure accuracy, relevance, and clarity. From insightful educational topics to engaging discussions, JAIN PU College's content is crafted to inform, inspire, and add value to its readers, reflecting the institution's commitment to intellectual growth and innovation.
View all Blogs