
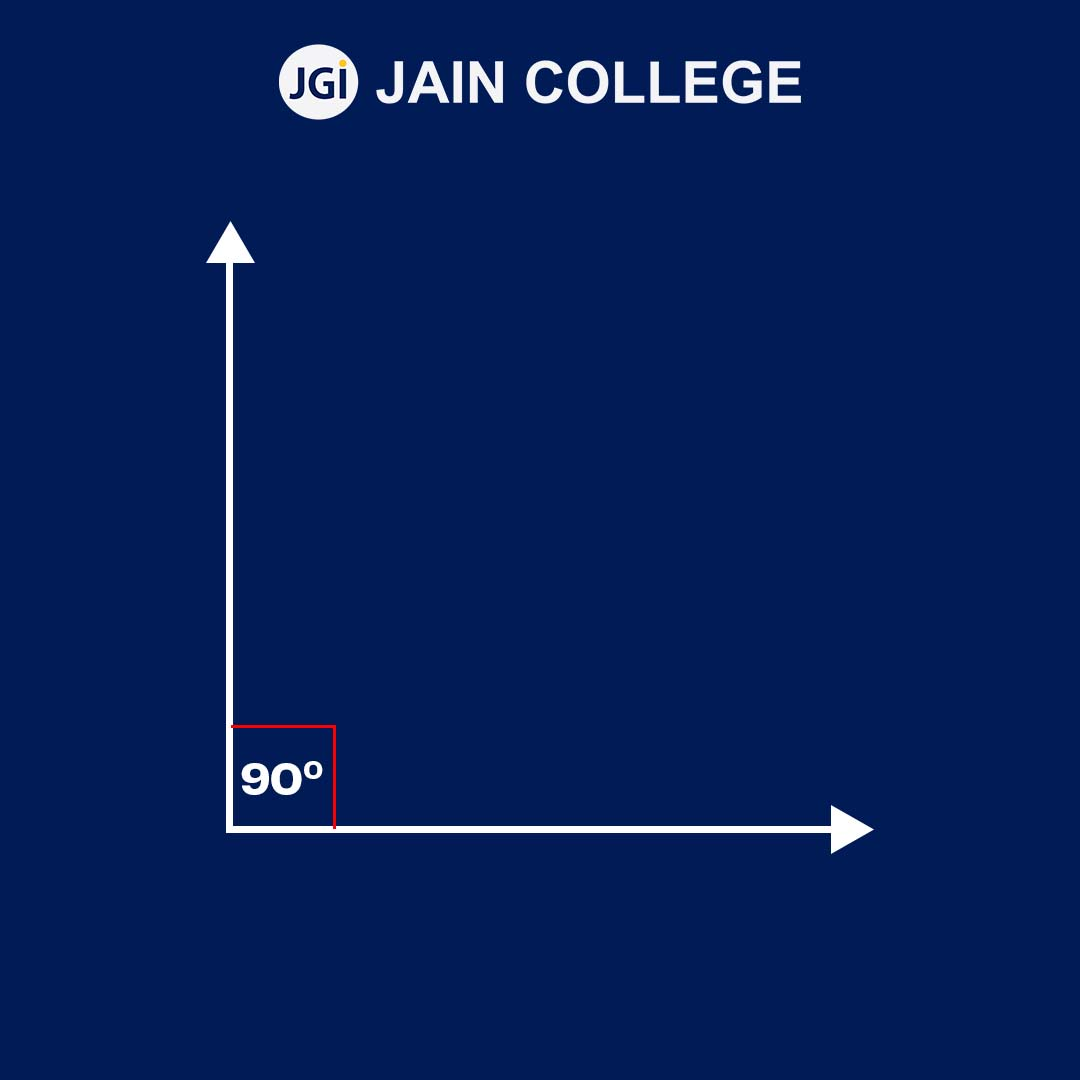
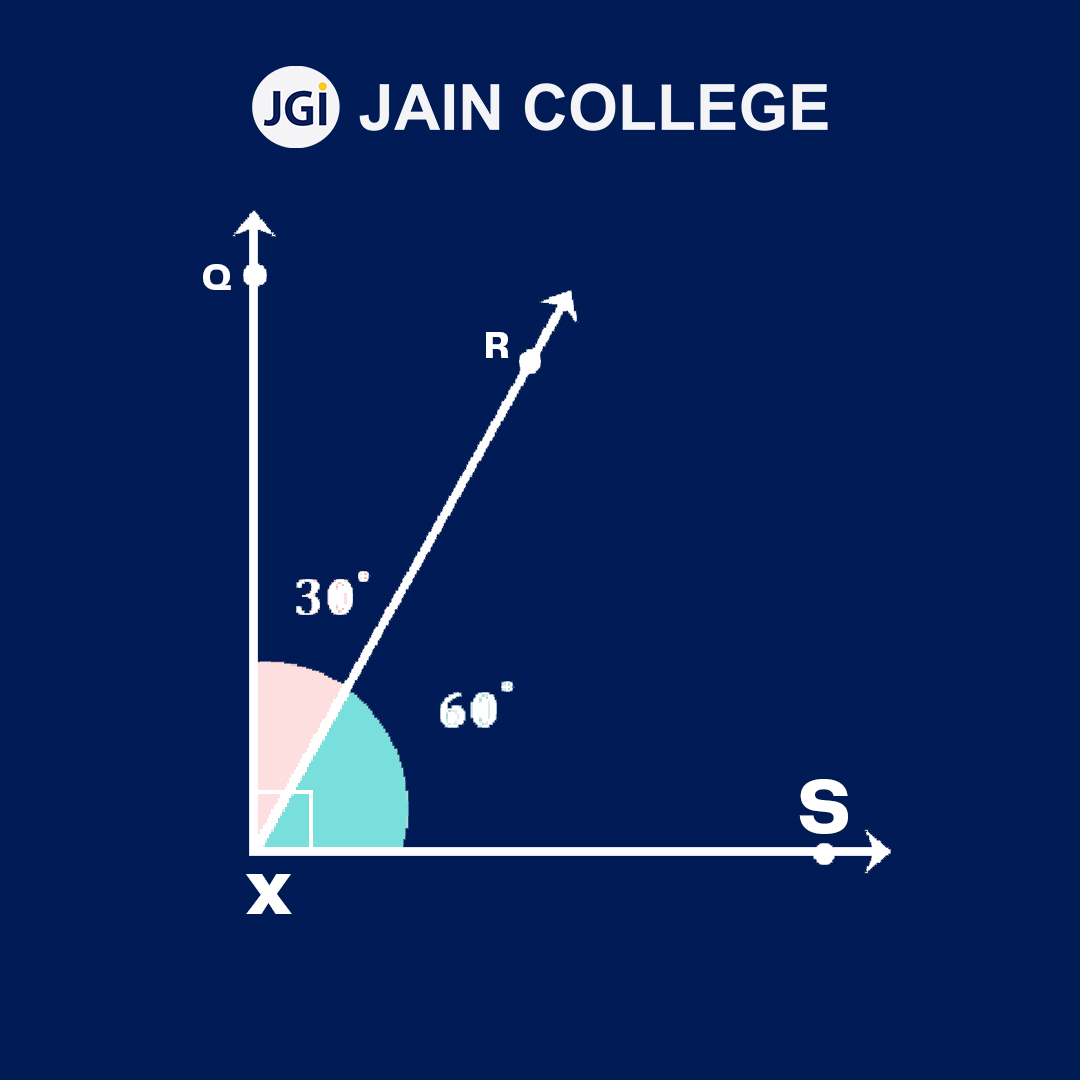
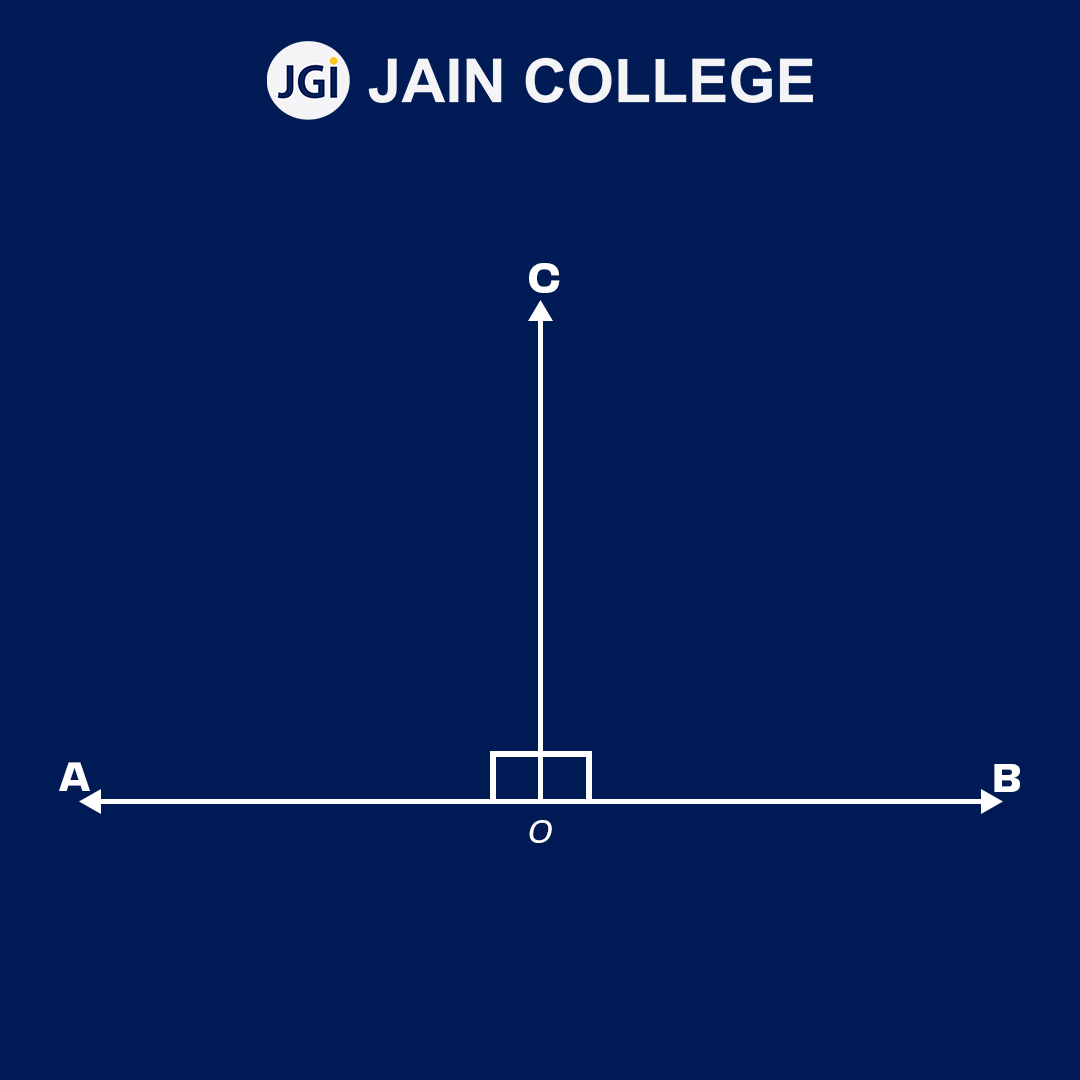
A right angle has an angle that measures exactly 90 degrees.
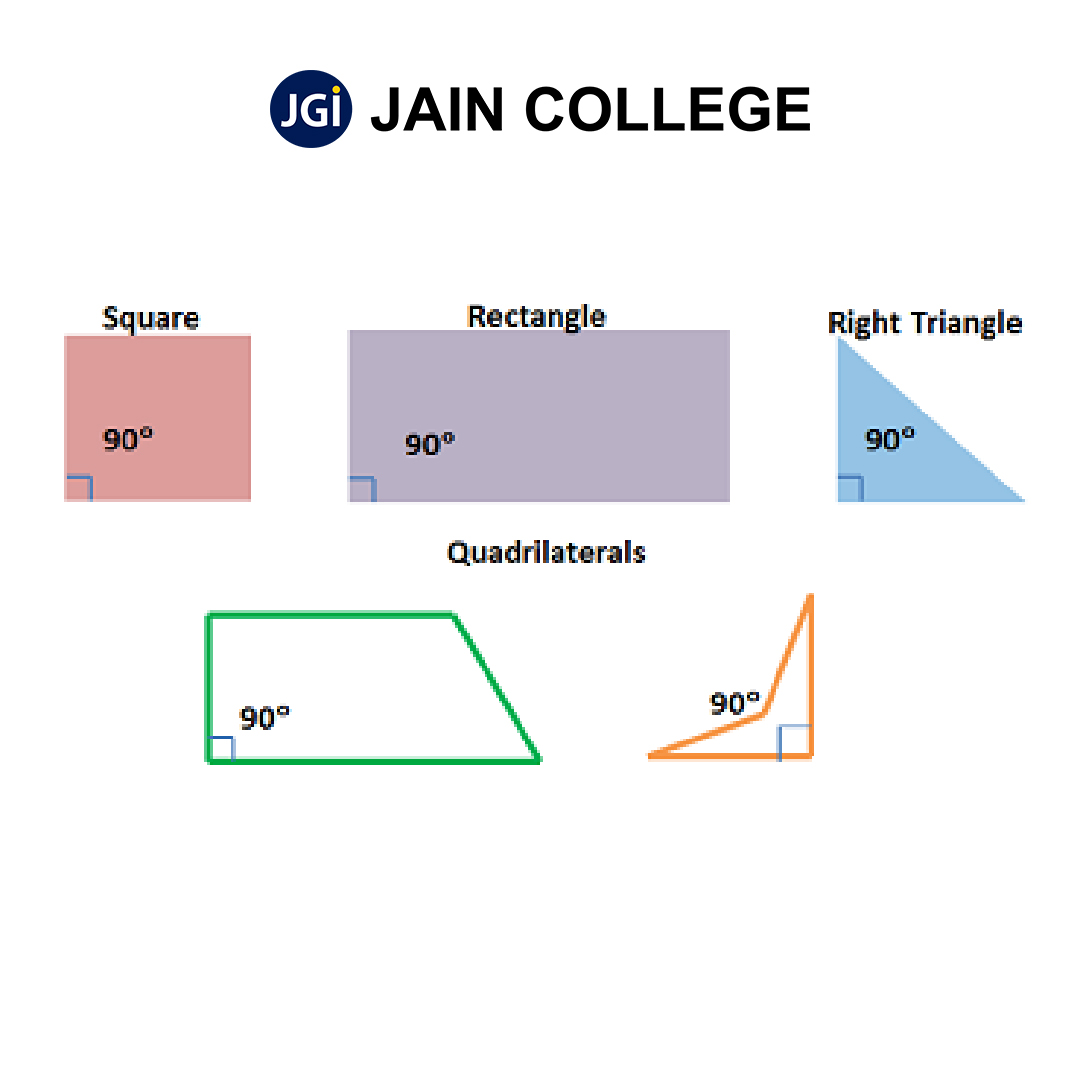
Right angles are observed in polygons such as triangles, squares, rectangles and other quadrilaterals. The symbol ‘?’ denotes the 90o angle.
Right angles are among the most commonly observable angles around us. It can be seen in door frames, book corners or a cardboard among others.
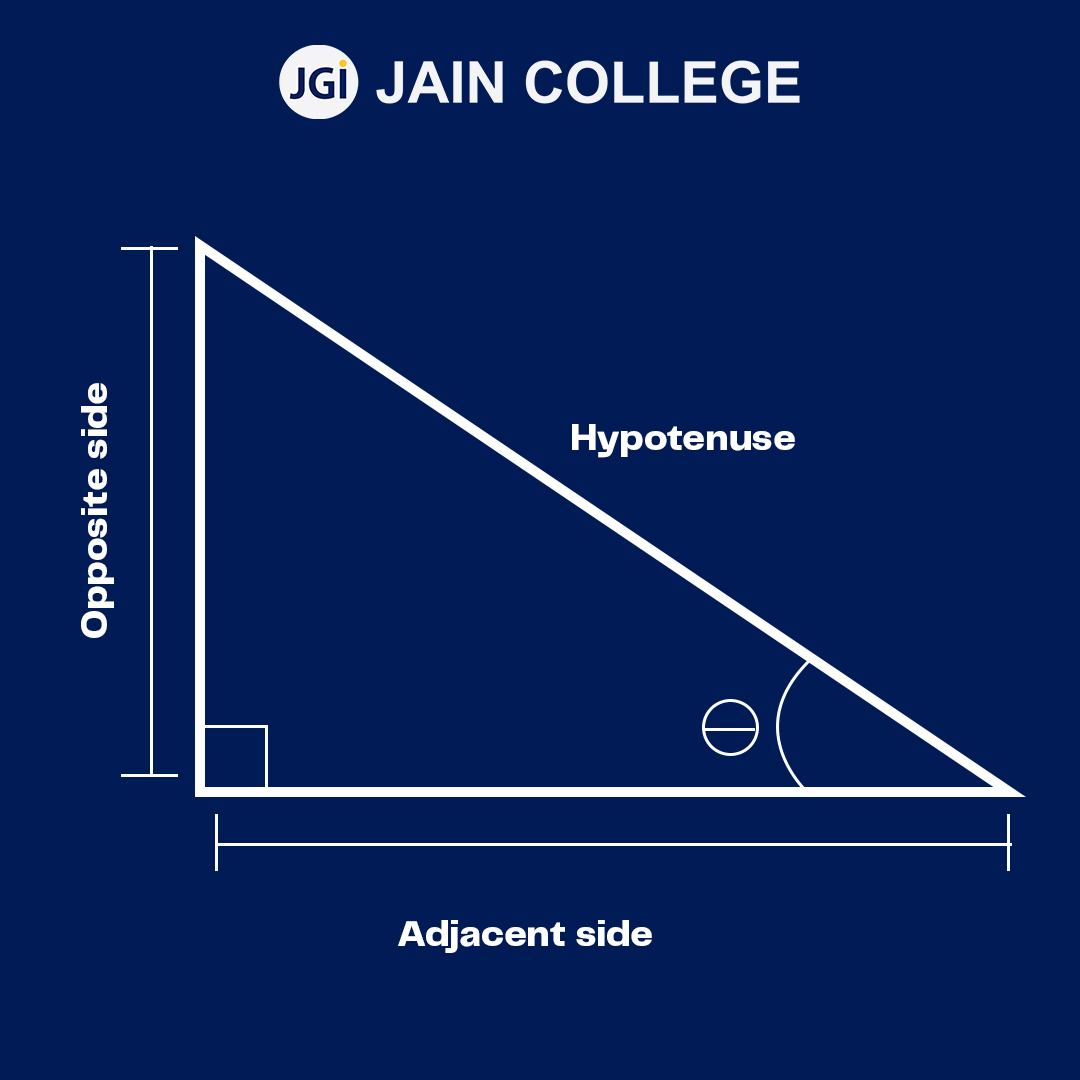





The Pythagorean theorem states in a right-angled triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides.
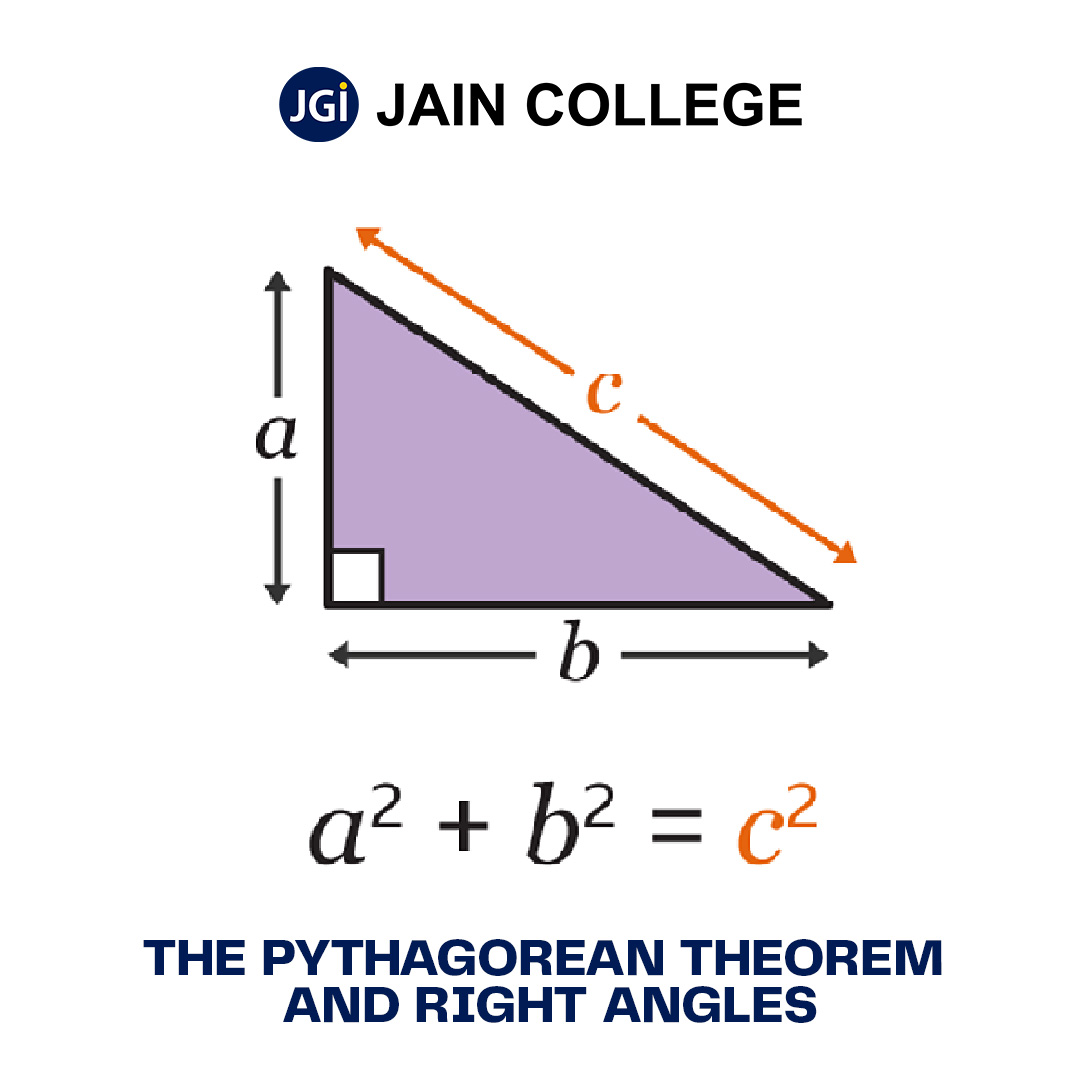
In the above right-angle triangle ?ABC –
c2 = a2 + b2??
Here, ????
b is the base,
a is the perpendicular (height)
c is the hypotenuse
Example: Two beams are placed perpendicular to one another such that they form a right angle at their point of intersection. If beam 1 is 6 feet and beam 2 is 8 feet, what will be the measure of the support beam?
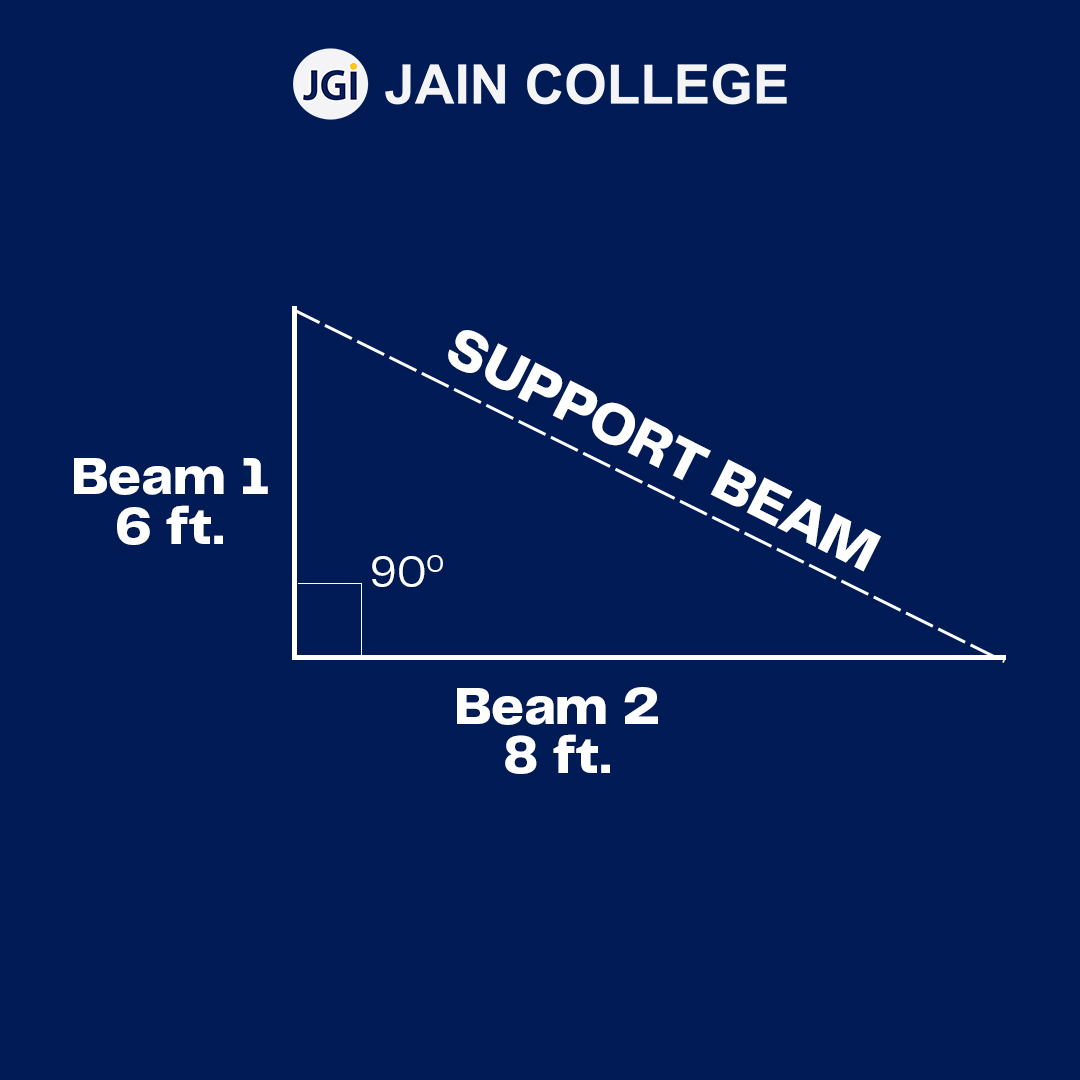
In the above problem, beam 1 is the altitude and beam 2 is the base of a right-angle triangle. So, the support beam which is opposite to the right angle will form the hypotenuse.
As per Pythagoras theorem,
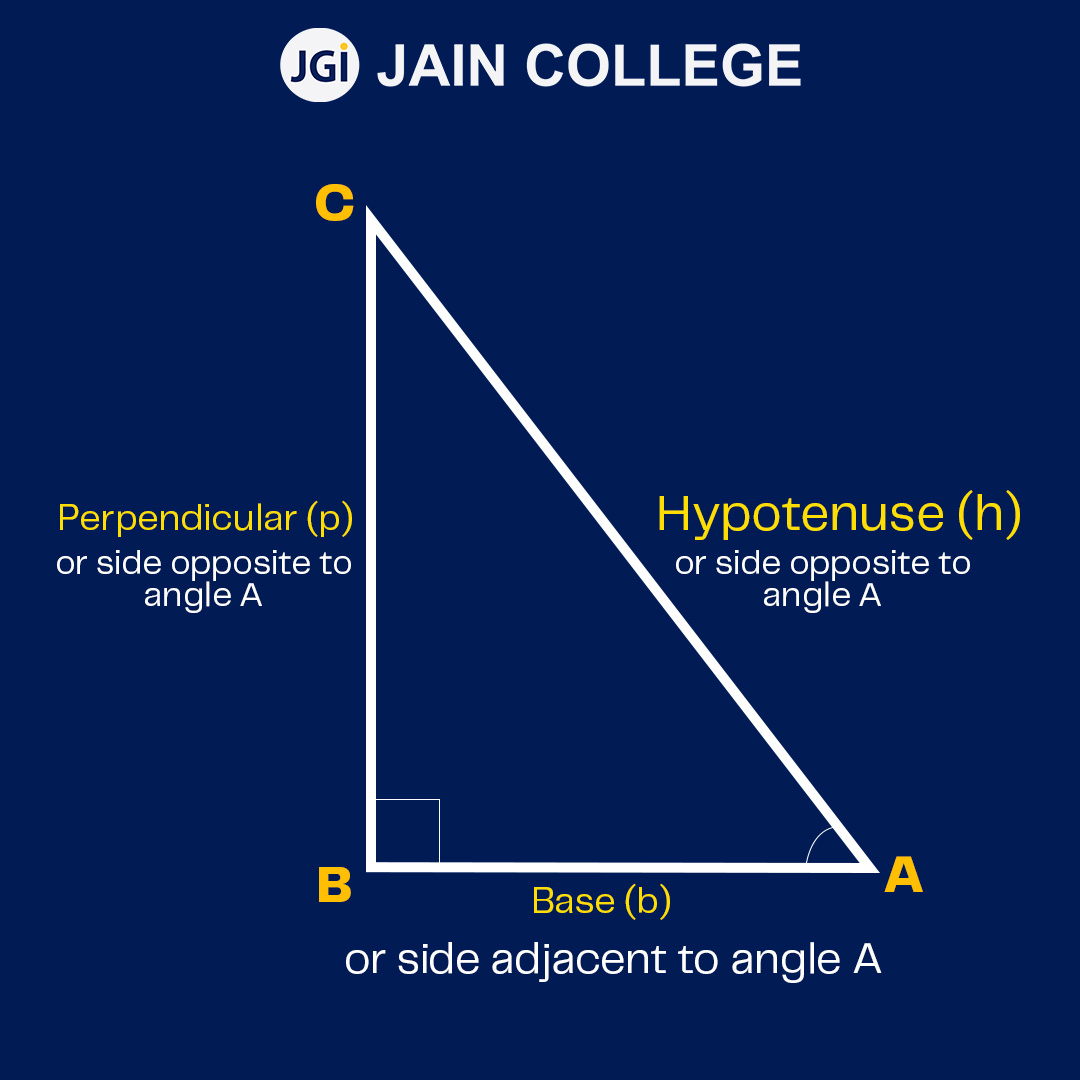
h2 = p2 + b2
thus,
support beam = (6)2 + (8)2
= 36 + 64
= 100
Thus, the measure of the support beam is 100 feet.
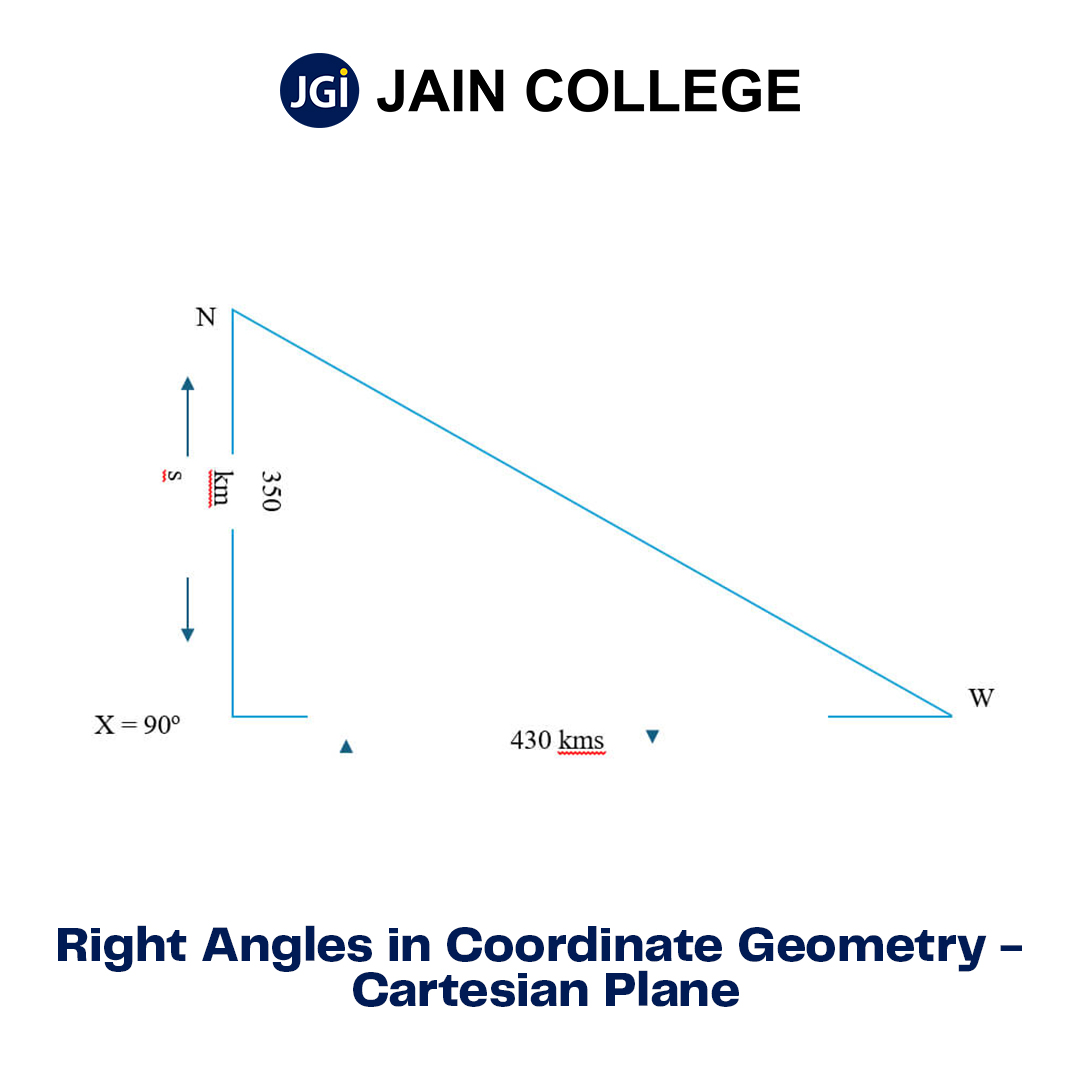
Pythagoras theorem is extensively used by architects and civil engineers in the construction of buildings, bridges, roofs etc. In two-dimensional navigation, the Pythagorean theorem helps in finding the shortest distance between two lengths. For instance, on a sea route, if the captain is navigating to a point that is 350 km north and 430 km to the west. To understand the distance from the ship to the point and calculate how many degrees to the west from the north the ship would need to follow to reach that point.
N
If the point of intersection of the north leg and the west leg is considered to be x and it forms a right angle, then the shortest line connecting them will be the hypotenuse. This principle can be used for air navigation. For instance, a plane can use its height above the ground and its distance from the landing lane at the airport to find the correct place to begin a descent to that airport.
In coordinate geometry, you can identify and work with right angles on the Cartesian plane. This is done by understanding relationships between lines and applying geometric properties. Right angles are crucial in coordinate geometry, particularly when defining axes (x-axis and y-axis) and plotting points.
The Cartesian Coordinate System is also known as the rectangular coordinate system because of the right angles formed by the axes and grid lines. The two-dimensional plane where the x-axis and y-axis meet at a right angle is called the origin. Further, each horizontal line in the grid intersects each vertical line in the grid at a right angle. The Cartesian Coordinate System is fundamental in fields like computer graphics, navigation, and design, where precise measurements and perpendicularity are required.
The 2-D cartesian coordinates are often used on maps to identify the equator, latitude and longitude. The individual grids are also used for plotting areas and identifying landmarks among others.

In the above diagram, a is the perpendicular, and b is the base. The side c forms the hypotenuse which is formed at the points (3,5) and (-1,2). The right angle is created at the point (3, -1) where a and b meet.
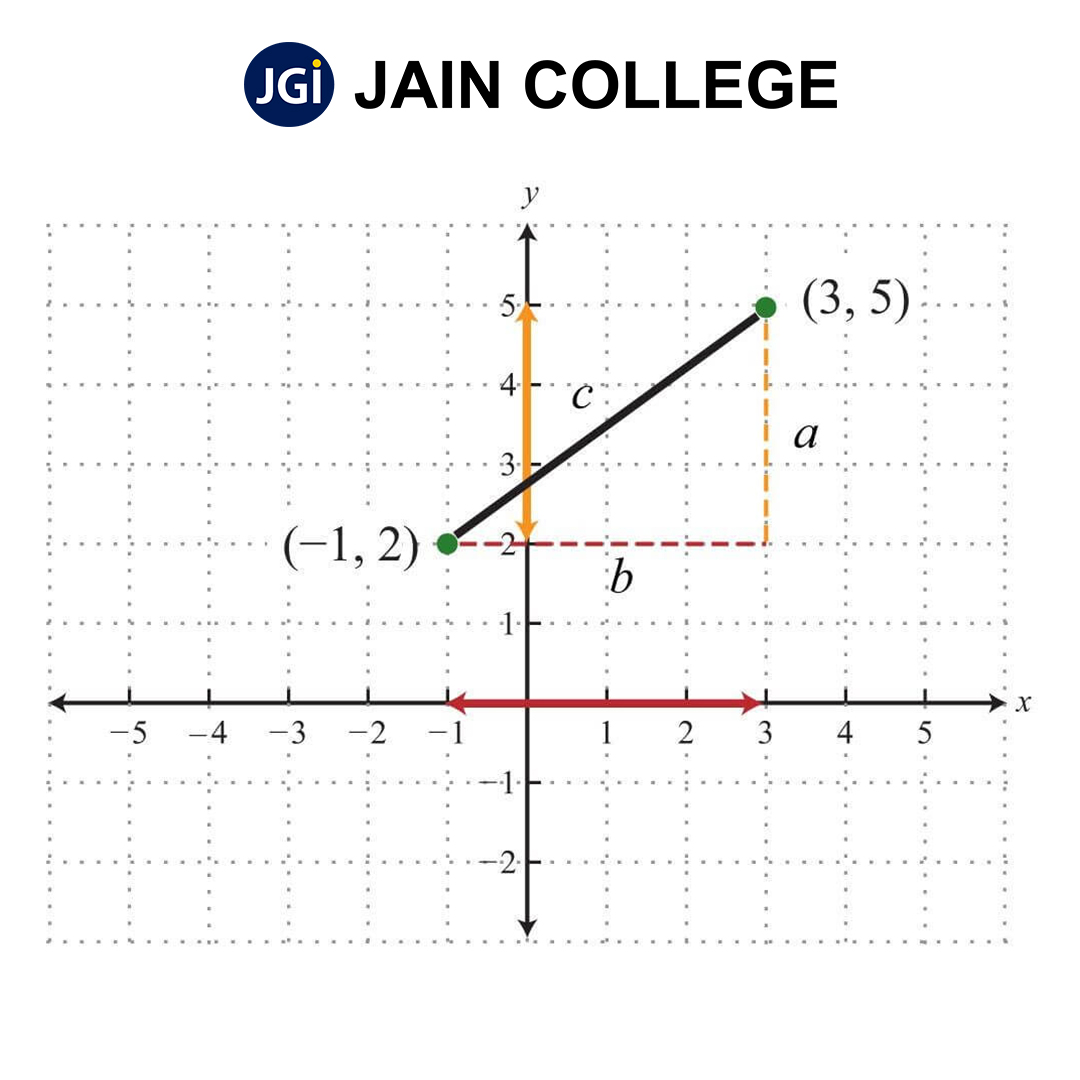
If we apply the Pythagorean theorem, ????2 + ????2 = ????2, to find the hypotenuse, ????, with ????=3 and b = 4 units.
????2 = (3)2 + (4)2
= 9 + 16
= 25
Therefore,
c = ?25
= 5
Therefore, the hypotenuse, which is the distance between the two points, can be written as 5 units.

JAIN PU College, a part of the renowned JGI Group, is committed to empowering students with quality education.
Beyond academics, the college ensures its online content reflects the same standard of excellence. Every blog and article is meticulously vetted and proofread by subject matter experts to ensure accuracy, relevance, and clarity. From insightful educational topics to engaging discussions, JAIN PU College's content is crafted to inform, inspire, and add value to its readers, reflecting the institution's commitment to intellectual growth and innovation.
View all Blogs