
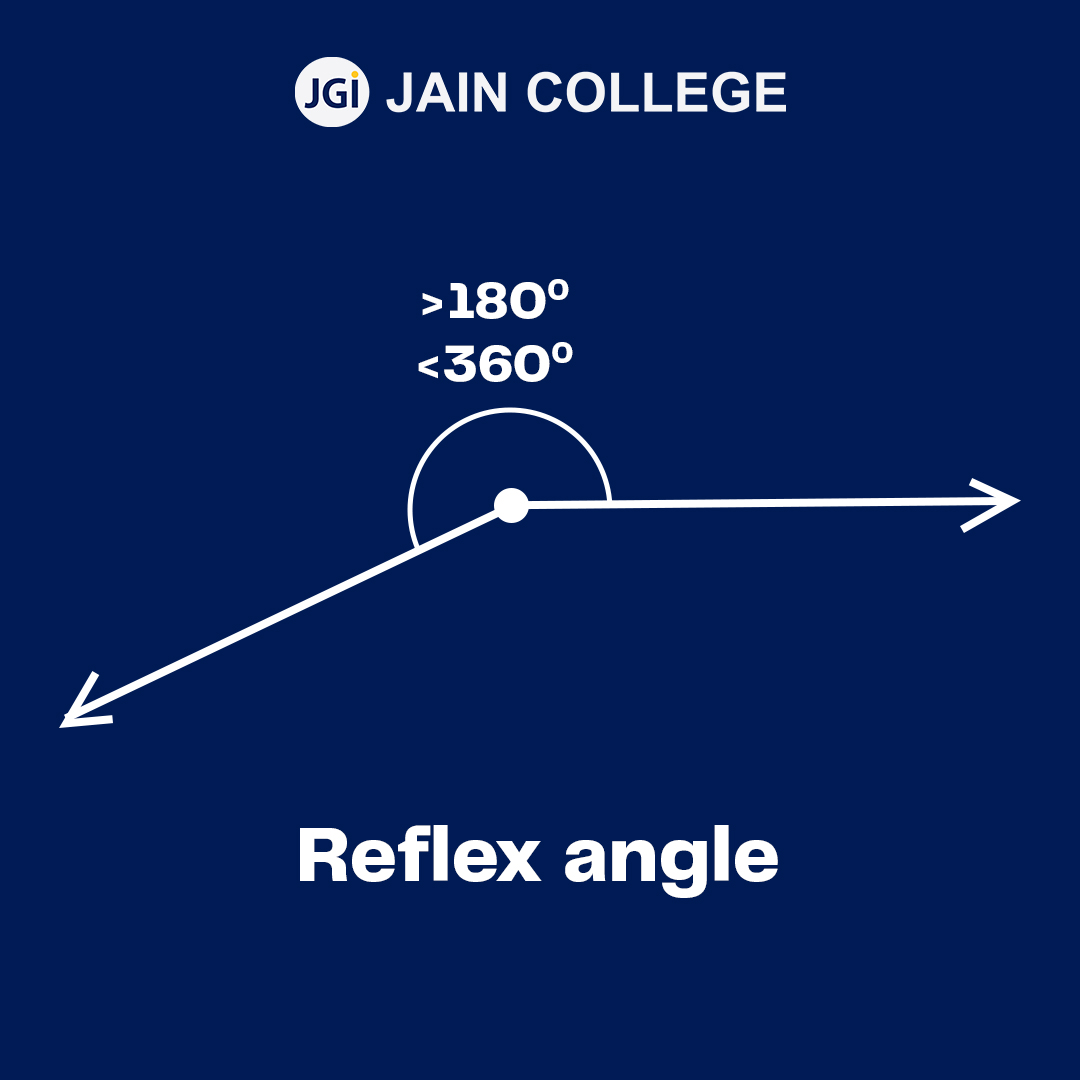
A reflex Angle is an angle that measures more than 180 degrees but less than 360 degrees. It is characterised by a wide opening that spans more than half of a circle.
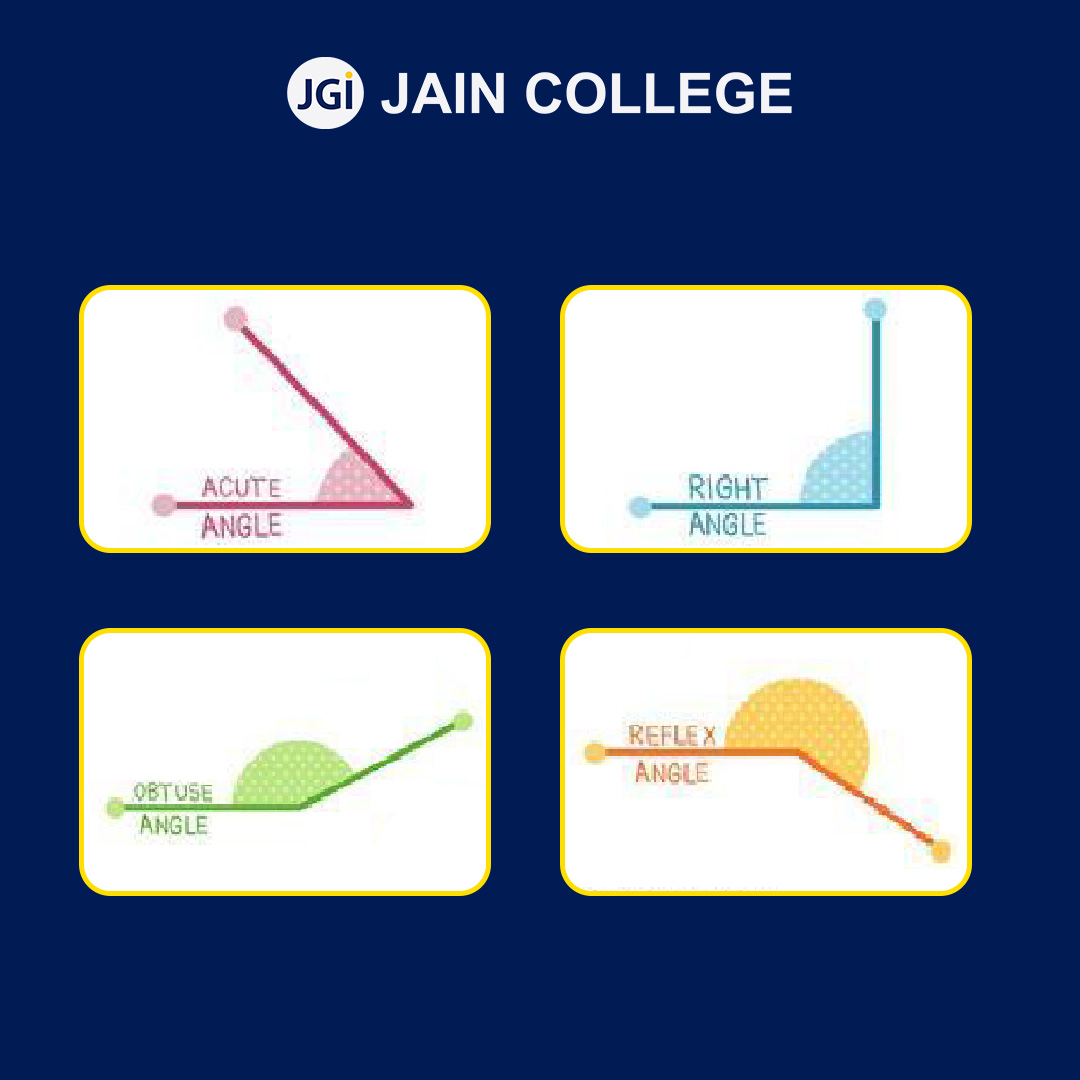
For every acute or obtuse angle, there is a reflex angle –
A polygon is a closed plane figure such as a square, triangle, or pentagon, with three or more sides that are all straight. If a polygon has at least one reflex angle in its interior, then it is called a concave polygon.

Concave polygons are generally irregular.
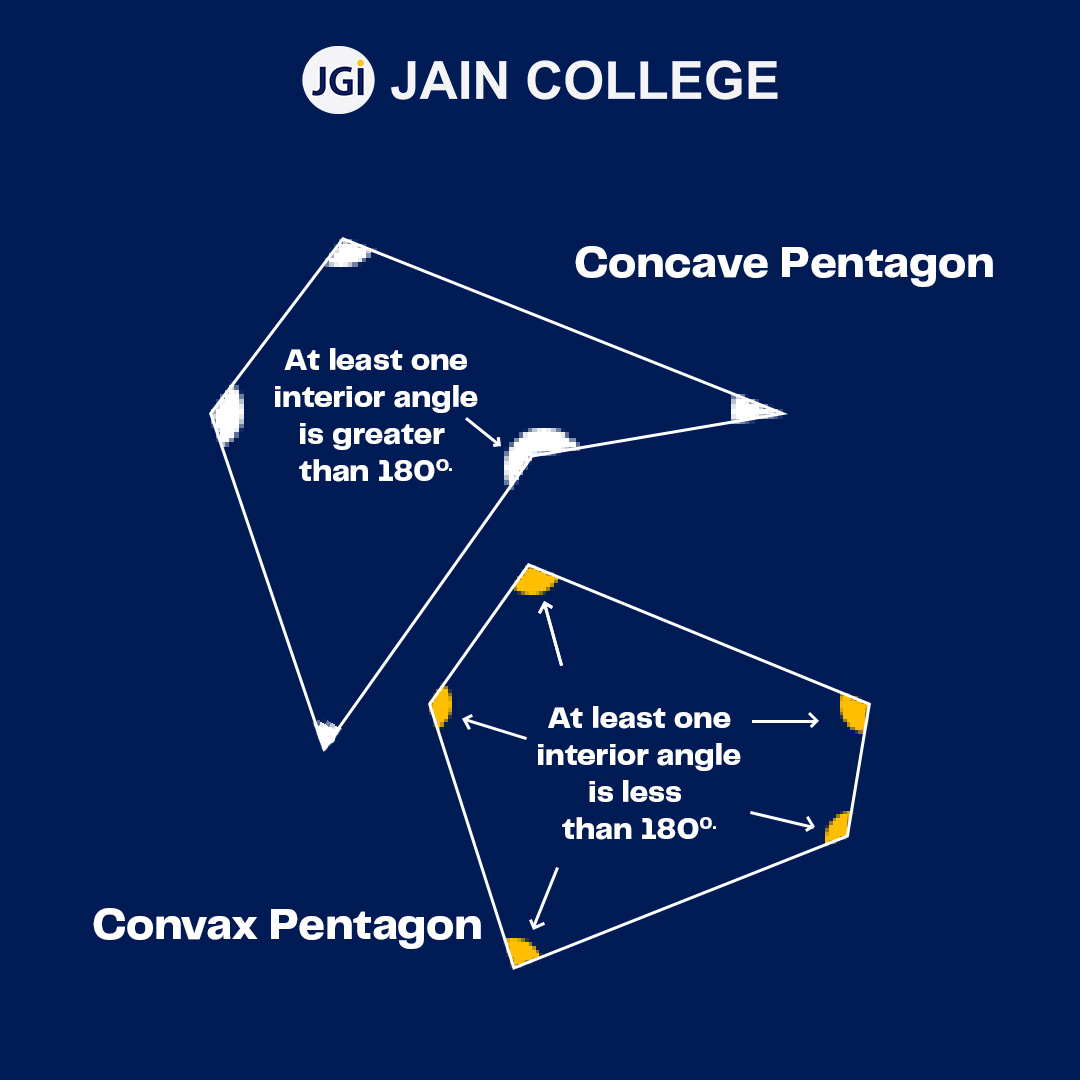
Where a convex polygon has all its angles less than 180°, a concave polygon is opposite to a convex polygon.
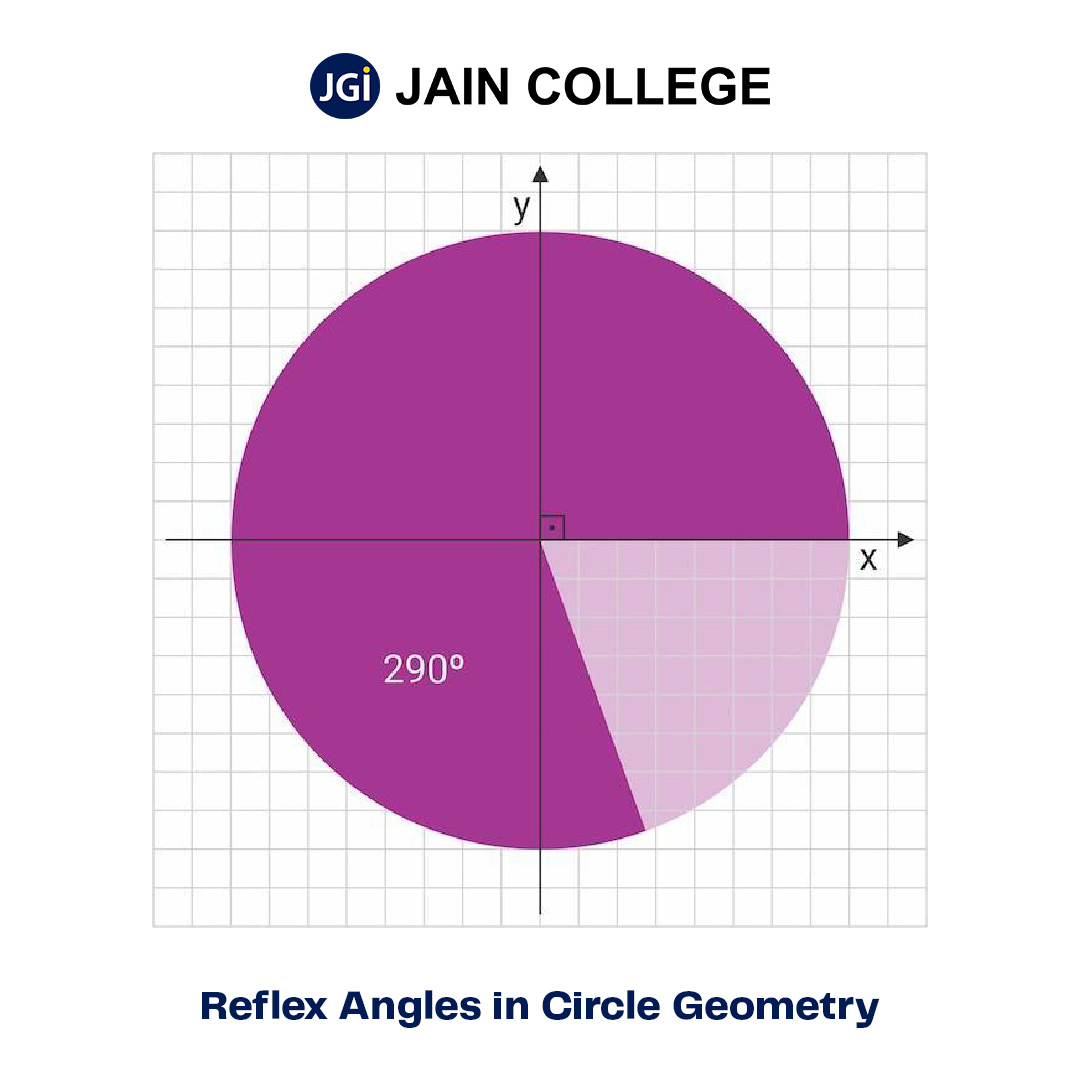
Unlike acute or obtuse angles, which are smaller than a straight angle, a reflex angle “wraps” around a central point and covers more than half of the circle. In circular geometry, reflex angles represent a larger portion of the circle and are encountered when dealing with sectors, arcs, and rotational movement. For example, if two radii are drawn from the centre of a circle to its circumference, the angle between them can either be the smaller, interior angle or the larger, reflex angle.

Reflex angles allow us to analyse rotations greater than a half-turn and provide insight into angular measurements in circular paths, which are common in fields like engineering, physics, and navigation.

To measure the reflex angle, calculate the interior angle and subtract the value from 360°. A protractor is used to measure the angle.
Reflex Angle = 360° - Interior Angle
For instance,
The interior angle of the above figure is 150o. Then the value of the external reflex angle is,
xo = 360o – 150o
= 210o.

The Unit Circle is a visual representation of “special angles”, which are the standard angle values of all the trigonometric ratios. It is called the “unit” circle since the measure of its radius is 1. The Unit Circle shows trigonometric values for the angles. The entire unit circle has a complete angle of 360º, and the four quadrant lines of the circle make angles of 90º, 180º, 270º, and 360º(0º). The reflex angles appear on the third and fourth quadrants where the angles are between 180° and 360°.
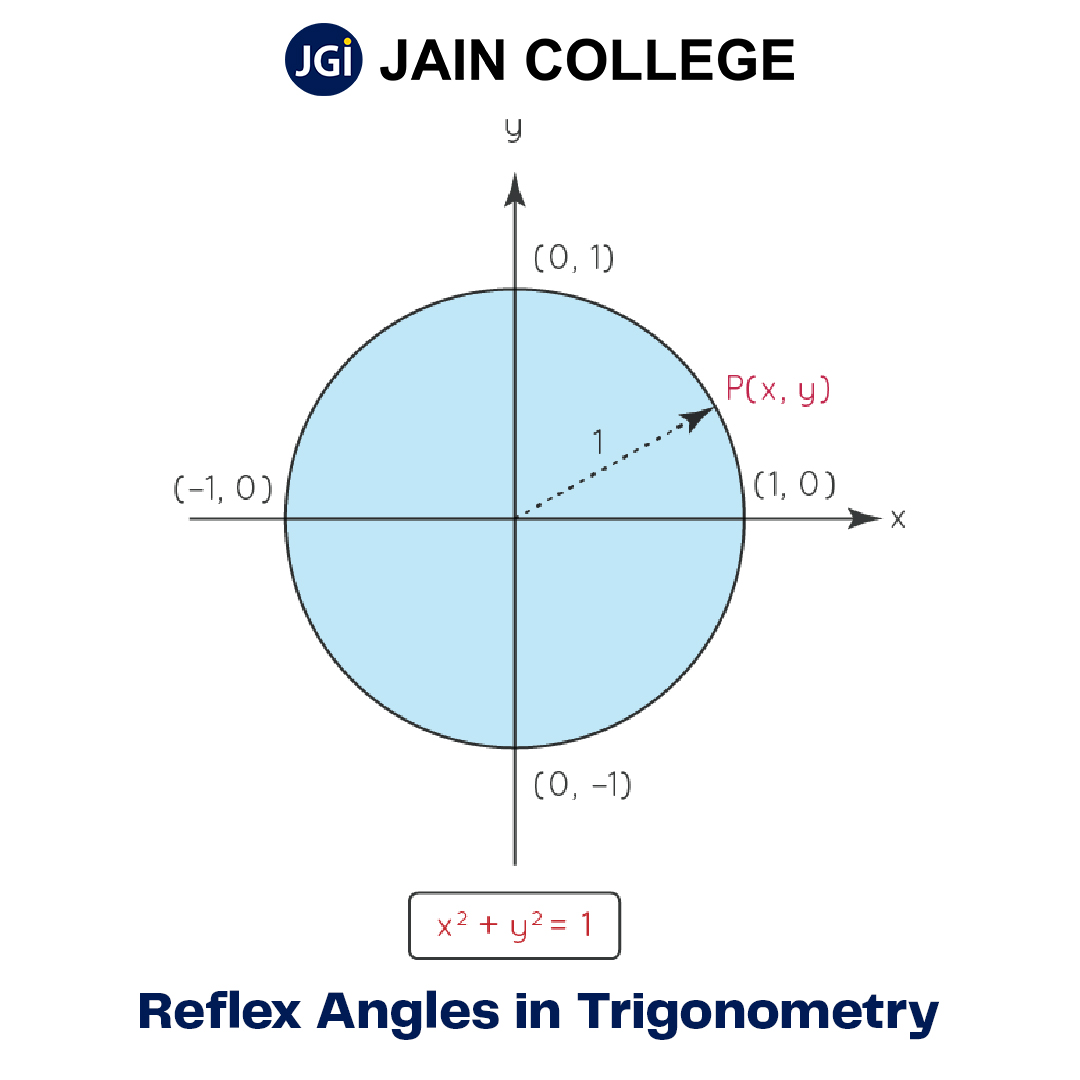
Any point on the unit circle has coordinates (x, y), which are equal to the trigonometric identities of (cosθ, sinθ). If cosθ = x, and sinθ = y, these values can be used to compute the other trigonometric ratio values. Thus,
tanθ = sinθ/cosθ
The radius value in the unit circle is 1, and the value of Sinθ and cosθ values always lie between 1 and -1. At 90º and at 270º the cosθ value is equal to 0 and hence the tan values are undefined
In periodic functions like sine, cosine, and tangent functions, reflex angles help understand periodicity and symmetry in trigonometric graphs. For instance, the sine and cosine functions repeat every 360°, so reflex angles help describe points along these cycles. They affect the sign and values of trigonometric functions because in the third and fourth quadrants, the sine and cosine take on negative values.
Angles represent positions around a circle in a circular motion. Reflex angles help describe positions beyond the 180° mark, which is useful for tracking an object’s position around the full circumference. They are particularly relevant in phase calculations, where angles determine the position and direction of a rotating object. For example, an object at 345° is in the fourth quadrant of the circle, which affects its coordinate signs (positive and negative in the Cartesian plane).
Reflex angles describe rotation from an initial position (positive x-axis) and help model orientations that exceed 180°. It helps in describing rotations in the counterclockwise direction where movements are often measured from 0° to 360°. For example, a rotation of 260° would be a reflex angle, indicating the object has rotated more than a half-turn but not yet a full turn.
Some common examples of the application of reflex angles can be seen in –

Clock arms when they rotate around the axis to show different times.

In Yoga studios when students make asanas such as the Bow pose, Cobra Pose, Surya namaskar, etc.

Many crossroads and road intersections have reflex angles
Q1. If sinθ = −0.5 and θ is a reflex angle, find the values of θ in degrees.
Solution 1:
Since θ is a reflex angle, we know 180? < θ < 360o
sinθ = −0.5
We can find the corresponding acute angle by solving sin α = 0.5.
This gives us -
α = 30o
Since θ is negative, it must lie in the third or fourth quadrant of the unit circle.
Hence,
The value of θ in degrees is 210o or 330o.

JAIN PU College, a part of the renowned JGI Group, is committed to empowering students with quality education.
Beyond academics, the college ensures its online content reflects the same standard of excellence. Every blog and article is meticulously vetted and proofread by subject matter experts to ensure accuracy, relevance, and clarity. From insightful educational topics to engaging discussions, JAIN PU College's content is crafted to inform, inspire, and add value to its readers, reflecting the institution's commitment to intellectual growth and innovation.
View all Blogs