
When the coplanar lines are intersected by a transversal, internal angles and external angles are formed at the points of intersection. Alternate angles occur on the opposite sides of a transversal line and are of the same size. They are non-adjacent angles that occur when a straight line, called a transversal line, intersects two parallel lines.
In the given figure, ab and cd are two parallel lines.
xy is the transversal line that intersects both lines – ab and cd.
When two parallel lines are cut by a transversal, then the alternate angles are equal.
Therefore,
∠1 = ∠8
∠2 = ∠7
∠3 = ∠6
∠4 = ∠5
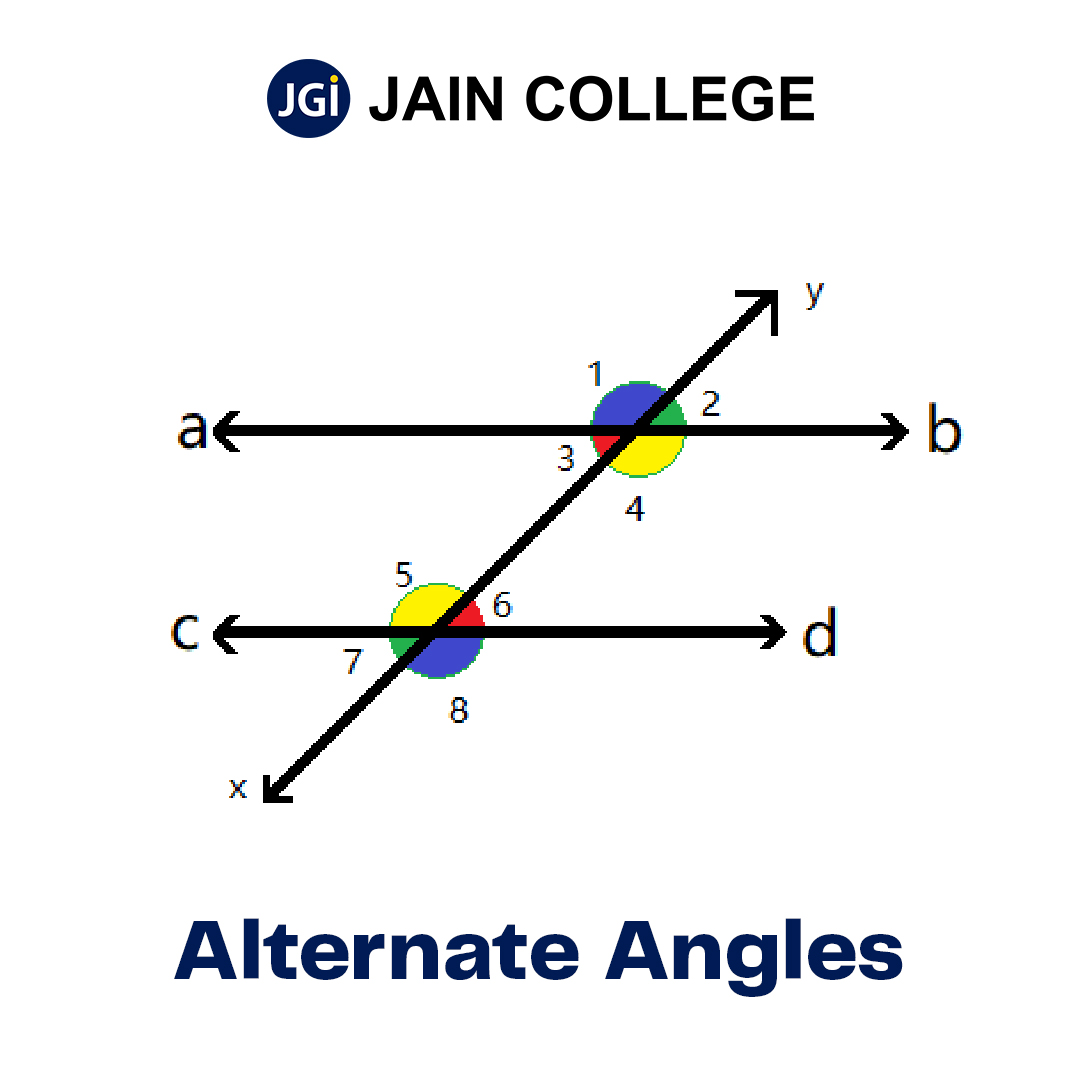
When two coplanar parallel lines ab and cd have a line xy intersect them acting as a transversal line, the figure creates 8 angles.
∠3 + ∠4 = 180o ---- (1)
∠2 + ∠4 = 180o ---- (2)
When we consider (1) and (2),
∠2 = ∠3
Similarly,
∠5 + ∠6 = 180° ---- (3)
∠8 + ∠6 = 180° --- (4)
When we consider (3) and (4),
∠5 = ∠8
Since they are corresponding angles,
∠2 =∠6 and ∠4 = ∠8
Which means,
∠3 =∠6 and ∠4 = ∠5
Where, ∠3, ∠4, ∠5, and ∠6 are alternative angles.
Thus, opposite angles are either congruent or equal.
There are two types of angles based on their position –
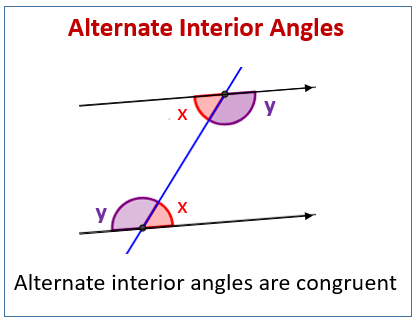
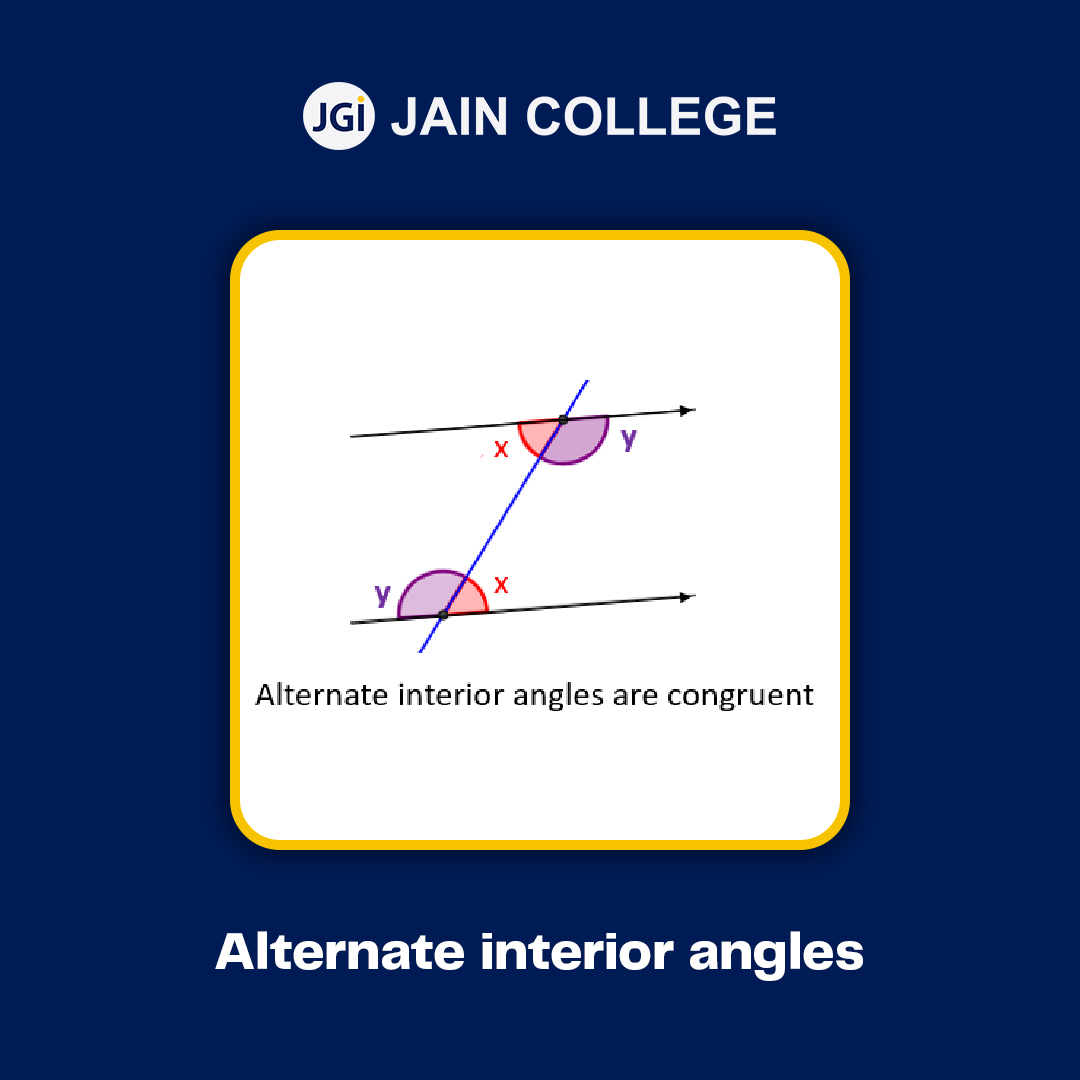
Alternate interior angles are the pair of angles that occur on the interior side of the parallel line and the opposite side of the transversal. In the above figure, the alternate interior angles are –
∠3 = ∠6
∠4 = ∠5
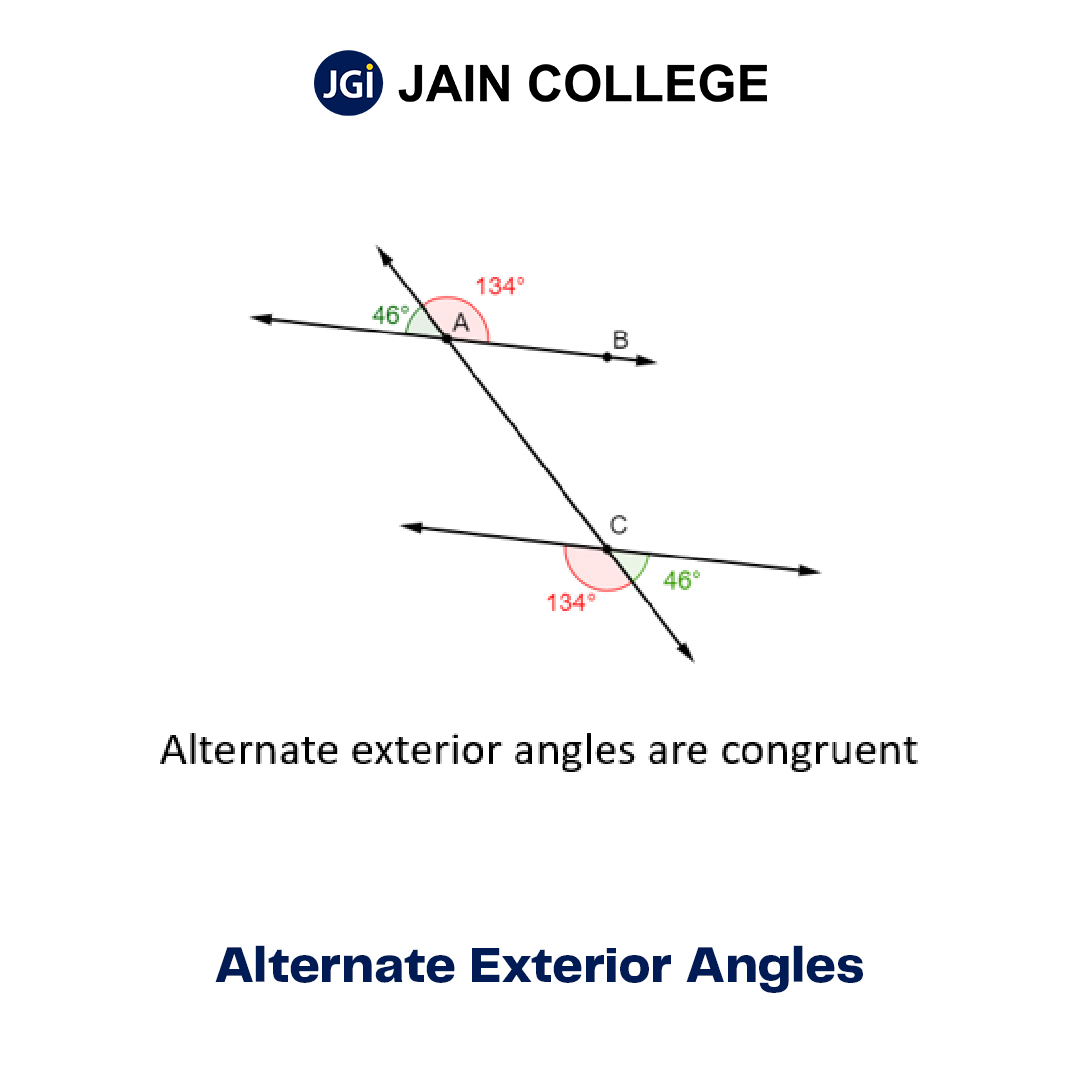
Alternate exterior angles are the pair of angles that occur on the exterior side of the two parallel lines and the opposite side of the transversal. In the above figure, the alternate exterior angles are -
∠1 = ∠8
∠2 = ∠7
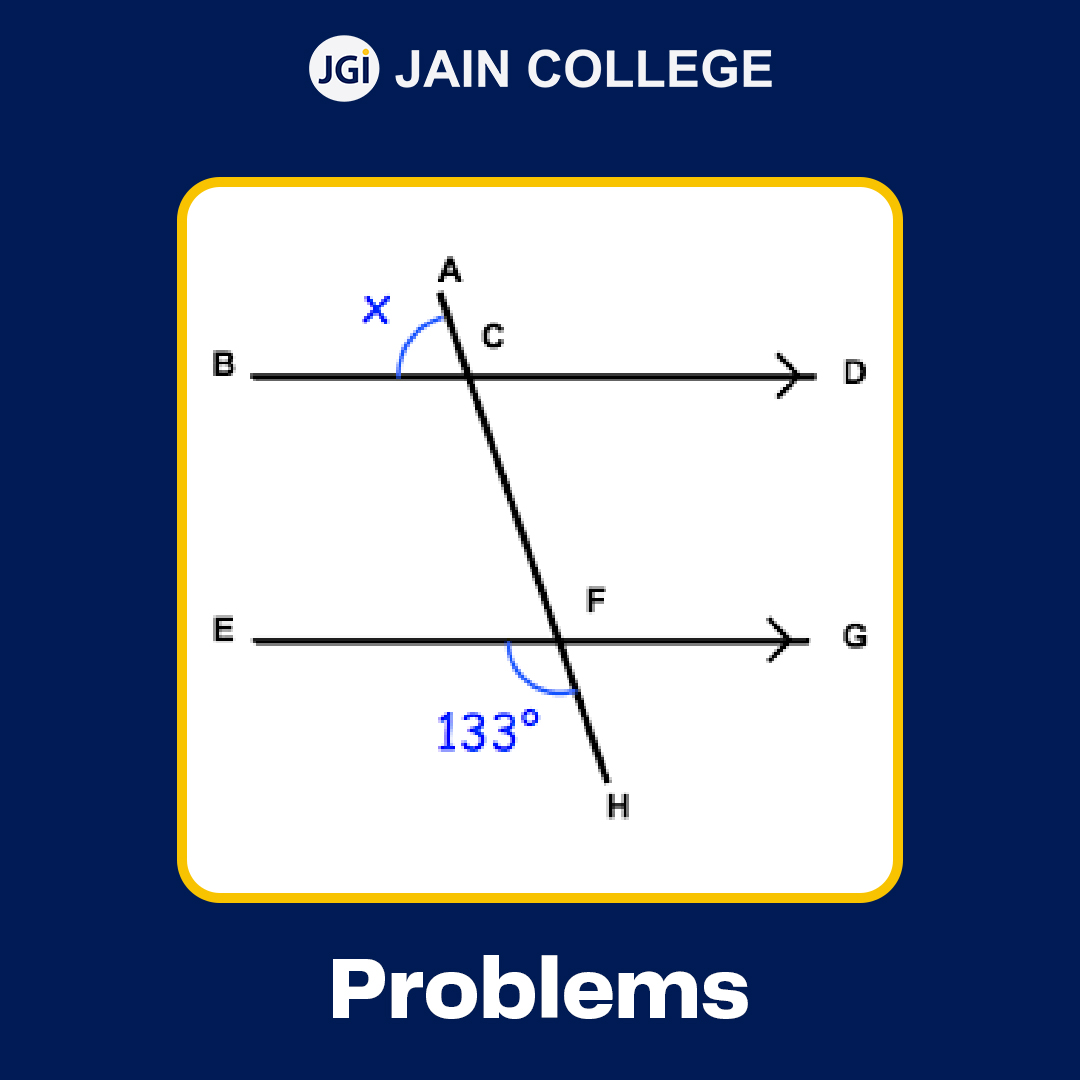
Q1.
If the angle ∠EFH = 133o, calculate the values of all the other angles in the above figure.
Solution 1:
Alternate angles are congruent. Therefore,
∠EFH = ∠ACD = 133o
The total value of corresponding angles is 180o. Therefore,
∠ACD + ∠ACB = 180o
133o + ∠ACB = 180o
∠ACB = 180o – 133o
= 47o
The alternate angle to ∠ACB is ∠GFH. Therefore,
∠ACB = ∠GFH = 47o
The corresponding angle to ∠GFH is ∠GFC. Therefore, its value is 133o.
The alternate angle to ∠GFC is ∠BCF. Thus,
∠GFC = ∠BCF = 133o
Q2.
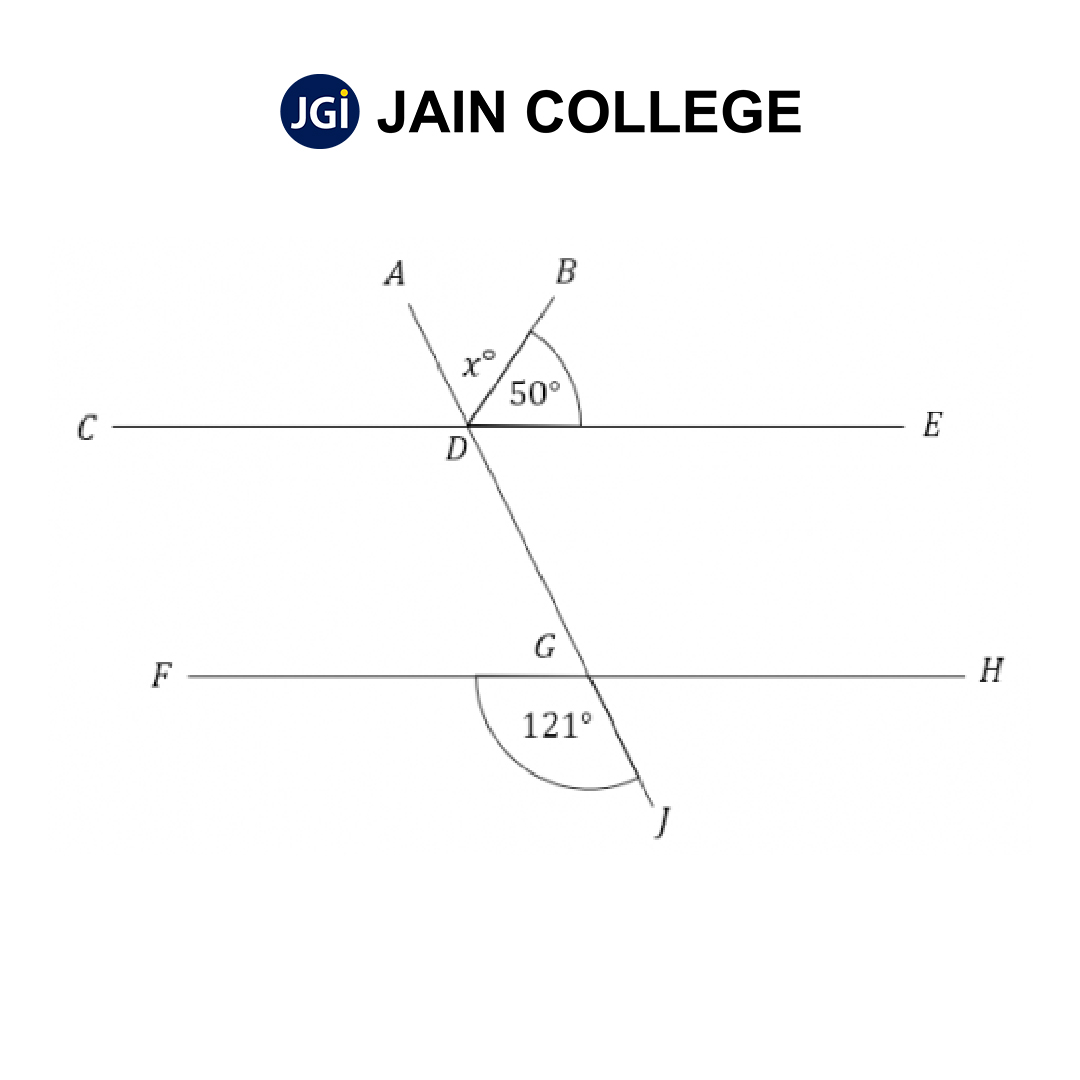
In the above diagram, ∠JGF is 121o and ∠BDE. Is 50o. Find the value of ∠ADB.
Solution 2:
∠JGF and ∠ADE are alternate angles. Therefore, they are congruent. Thus,
If ∠JGF = 121o,
Then ∠ADE = 121o
∠ADE = ∠ADB + ∠BDE
121o = xo + 50o
xo = 121o - 50o
= 71o
∠ADB = 71o

JAIN PU College, a part of the renowned JGI Group, is committed to empowering students with quality education.
Beyond academics, the college ensures its online content reflects the same standard of excellence. Every blog and article is meticulously vetted and proofread by subject matter experts to ensure accuracy, relevance, and clarity. From insightful educational topics to engaging discussions, JAIN PU College's content is crafted to inform, inspire, and add value to its readers, reflecting the institution's commitment to intellectual growth and innovation.
View all Blogs